RegBN: Batch Normalization of Multimodal Data with
Regularization

Morteza Ghahremani

Christian Wachinger

Munich Center for Machine Learning (MCML)

Technical University of Munich (TUM)

Munich, Germany

[Paper & Supplementary]

[Poster]

[Code]

Abstract

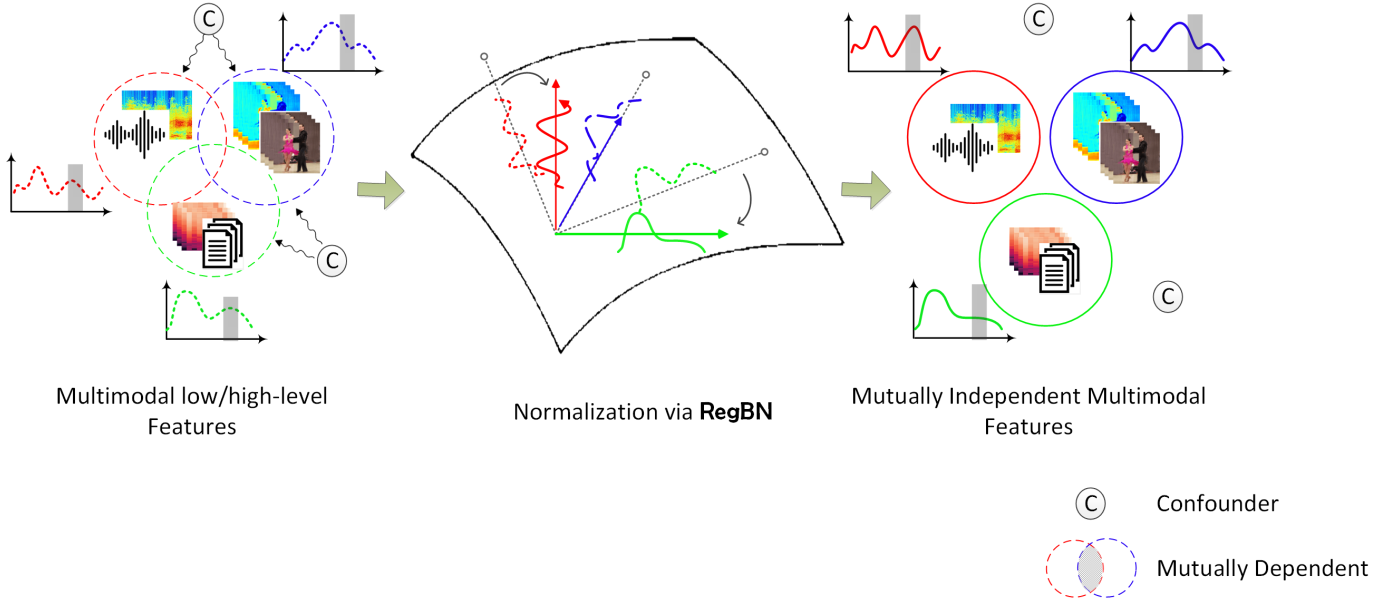
This paper introduces a novel approach for the normalization of multimodal data, called RegBN, that incorporates regularization. RegBN uses the Frobenius norm as a regularizer term to address the side effects of confounders and underlying dependencies among different data sources. It enables effective normalization of both low and high-level features in multimodal neural networks.

RegBN is batch normalisation method for multimodal data
RegBN generalizes well across multiple modalities of any architecture such MLPs, CNNs, ViTs, etc

RegBN can be applied to a vast array of heterogeneous data types, including text, audio, image, video, depth, tabular, 3D MRI, etc

RegBN eliminates the need for learnable parameters, simplifying training and inference

Method

Given a trainable multimodal neural network (e.g., MLPs, CNNs, ViTs) with multimodality backbones $A$ and $B$. Let $f^{(l)}$ represent the $l$-th layer of network $A$ with batch size $b$ and $n_1\times...\times n_N$ features that are flattened into a vector of size $n$. In a similar vein, we define $g^{(k)}$ as the $k$-th layer of network $B$ with $m_1\times\ldots\times m_M$ features that are flattened into a vector of size $m$. RegBN make $f^{(l)}$ and $g^{(k)}$ mutually independent via $$F(W^{(l,k)},\lambda_{+}) = ||{f^{(l)}-W^{(l,k)} g^{(k)}}||^2_2+\lambda_{+} (||{W^{(l,k)}}||_F-1)$$ Where $W^{(l,k)}$ is a projection matrix of size $n\times m$ and ${\lambda}_{+}$ is a Lagrangian multiplier. $W^{(l,k)}$ and ${\lambda}_{+}$ are estimated via an innovative recursive-based algorithm.

Where is it advisable to apply RegBN?

(a) RegBN as a layer normalizer (b) Late fusion with RegBN

Experiments

In the paper, we reported the performance of RegBN over eight multimodal databases with various modalities, including multimedia, affective computing, robotics, healthcare diagnosis, etc.

MNIST

tSNE visualization of the features extracted from a-b) an unimodal image and an unimodal audio, and c-e) the multimodal model with different normalization methods. Each data point represents a sample

Multimedia (MM-IMDb)

Multi-label classification scores (F1 score) of baseline SMIL with/without normalization on the MM-IMDb dataset

More results and details can be found in the paper and its supplementary.

BibTeX


            @article{ghahremani2023regbn,
                  title={RegBN: Batch Normalization of Multimodal Data with Regularization},
                  author={Ghahremani, Morteza and Wachinger, Christian},
                  year={2023},
                  eprint={2310.00641},
                  archivePrefix={arXiv},
                  primaryClass={cs.CV}
            }

Acknowledgments

This project was founded by Munich Center for Machine Learning: MCML.